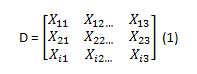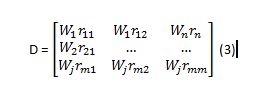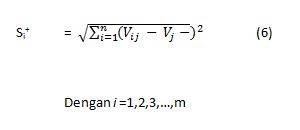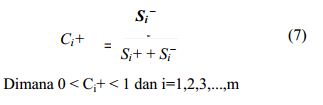JAWABAN QUIS ONLINE

SOAL QUIS ONLINE

Suatu kelurahan mendapatkan Bantuan Langsung Tunai dari pemerintah untuk masing masing kepala keluarga dengan syarat ketentuan sebagai berikut :

C1 : Jumlah Tanggungan
C2 : Pendapatan Kepala Keluarga
C3 : Luas Bangunan Rumah
C4 : Memiliki KK

Pilihlah 5 alternatif KK yang akan mendapatkan bantuan dari beberapa KK berikut ini :

Nama KK            C1    C2                     C3           C4
Aldyan                  4    2.350.000        100M2    Tidak Ada
Hendro                  5    3.050.000        50M2      Ada
Joko                      3    3.350.000        70M2      Ada
Doni                     4    2.550.000        90M2      Ada
Dono                    6    2.850.000        120M2    Ada
Kasino                 3    2.650.000        80M2      Ada
Susanto                2    3.350.000        150M2    Tidak Ada

Pembobotan dari kriteria diatas dapat dilihat dibawah ini :
C1 : Jumlah Tanggungan (Attribut Keuntungan)
1-2 : 1
3-4 : 2
5-6 : 3

C2 : Pendapatan Kepala Keluarga (Attribut Biaya)
2.000.000    : 1
2.400.000    : 2
2.800.000    : 3
3.200.000    : 4
3.600.000    : 5

C3 : Luas Bangunan Rumah (Attribut Biaya)
50-70    : 1
71-90          : 2
91-110        : 3
111-130      : 4
131-150      : 5

C4 : Memiliki KK (Attribut Keuntungan)
Ada     : 2
Tidak Ada    : 1

Penyelesaian  Dengan Metode Topsis

Alternatif	kriteria
	C1	C2	C3	C4
aldyan	2	1	3	1
Hendra	3	3	1	2
Joko	2	4	1	2
Doni	2	2	2	2
Dono	3	3	4	2

 

Bobot W=[4,5,4,3]

1.    Membuat matrik keputusan ternormalisasi

        

 

             

2.         Membuat matriks keputusan ternomalisasi berbobot

 Y11 = W1 R11 = 4 * 0,3651 = 1,4604

             Y21 = W1 R21 = 4 * 0,5477 = 2,1908

             Y31 = W1 R31 = 4 * 0,3651 = 1,4604

             Y41 = W1 R41 = 4 * 0,3651 = 1,4604

             Y51 = W1 R51 = 4 * 0,5477 = 2,1908

             Y12 = W2 R12 = 5 * 0,1601 = 0,8005

             Y22 = W2 R22 = 5 * 0,4804 = 2,402

             Y32 = W2 R32 = 5 * 0,6405 = 3,2025

             Y42 = W2 R42 = 5 * 0,3202 = 1,601

             Y52 = W2 R52 = 5 * 0,4804 = 2,402

             Y13 = W3 R13 = 4 * 0,5388 = 2,1552

             Y23 = W3 R23 = 4 * 0,1796 = 0,7184

             Y33 = W3 R33 = 4 * 0,1796 = 0,7184

             Y43 = W3 R43 = 4 * 0,3592 = 1,4368

             Y53 = W3 R53 = 4 * 0,7184 = 2,8736

             Y14 = W4 R14 = 3 * 0,2425 = 0,7275

             Y24 = W4 R24 = 3 * 0,4851 = 1,4553

             Y34 = W4 R34 = 3 * 0,4851 = 1,4553

             Y44 = W4 R44 = 3 * 0,4851 = 1,4553

             Y54 = W4 R54 = 3 * 0,4851 = 1,4553

3.         Menentukan matriks solusi ideal positif dan negatif

            Y1⁺ = Max { 1,4604 ; 2,1908 ; 1,4604 ; 1,4604 ; 2,1908 } = 2,1908

            Y2⁺ = Min { 0,8005 ; 2,402 ; 3,2025 ; 1,601 ; 2,402 } = 0,8005

            Y3⁺ = Min { 2,1552 ; 0,7184 ; 0,7184 ; 1,4368 ; 2,8736 } = 0,7184

            Y4⁺ = Max { 0,7275 ; 1,4553 ; 1,4553 ; 1,4553 ; 1,4553 } = 1,4553

               A⁺ = { 2,1908 ; 0,8005 ; 0,7184 ; 1,4553 }

            Y1^- = Min { 1,4604 ; 2,1908 ; 1,4604 ; 1,4604 ; 2,1908 } = 1,4604

            Y2^- = Max { 0,8005 ; 2,402 ; 3,2025 ; 1,601 ; 2,402 } = 3,2025

            Y3^- = Max { 2,1552 ; 0,7184 ; 0,7184 ; 1,4368 ; 2,8736 } = 2,8736

            Y4^- = Min { 0,7275 ; 1,4553 ; 1,4553 ; 1,4553 ; 1,4553 } = 0,7275

               A^- = { 1,4604 ; 3,2025 ; 2,8736 ; 0,7275 }

4. Menentukan jarak antara nilai setiap alternatif dengan matriks solusi ideal positif dan negatif

5. Mencari Prefensi

Sistem Pendukung Keputusan Metode ELECTRE (Elimination and Choice Translation Reality)

Electre merupakan salah satu metode dari sistem pendukung keputusan yang berbasis multi kriteria yang berasal dari EROPA sekitar tahun 1960-an. ELECTRE berasal dari kata ELimination Et Choix Traduisant la Realité (ELimination and Choice Expressing Reality).Metode Elektre dapat digunakan dalam melakukan penilaian dan perankingan berdasarkan kelebihan dan kekurangan melalui perbandingan berpasangan pada kriteria yang sama.

Menurut Janko dan Bernoider (2005:11), ELECTRE merupakan salah satu metode pengambilan keputusan multikriteria berdasarkan pada konsep outranking dengan menggunakan perbandingan berpasangan dari alternatif-alternatif berdasarkan setiap kriteria yang sesuai.

Metode ELECTRE digunakan pada kondisi di mana alternatif yang sesuai dapat dihasilkan. Dengan kata lain, ELECTRE digunakan untuk kasus-kasus dengan banyak alternatif namun hanya sedikit kriteria yang dilibatkan.

Suatu alternatif dikatakan mendominasi alternatif yang lainnya jika satu atau lebih kriterianya melebihi (dibandingankan dengan kriteria dari alternatif yang lain) dan sama dengan kriteria lain yang tersisa (Kusumadewi dkk, 2006).

ELECTRE digunakan untuk kasus-kasus dengan banyak alternatif namun hanya sedikit kriteria yang dilibatkan. Suatu alternatif dikatakan mendominasi alternatif yang lainnya jika suatu atau lebih kriteria melebihi(bandingkan dengan kriteria dari alternatif yang lain) dan sama dengan kriteria lain yang tersisa (Kusimadewi dkk, 2009)

Salah satu studi kasus yang pernah dilakukan yaitu dilatarbelakangi banyaknya varian sepeda motor lengkap dengan keunggulan masing-masing, sehingga para konsumen merasa kesulitan untuk menentukan pilihan. oleh karena itu dianggap perlu untuk membuat suatu sistem pendukung keputusan dengan metode ELECTRE, yang diharapkan dapat membantu pembeli speda motor dalam hal menentukan pilihan secara tepat dari beberapa alternatif pilihan yang ada

Langkah-langkah yang dilakukan dalam penyelesaian masalah menggunakan metode ELECTRE adalah sebagai berikut :

Langkah 1: Normalisasi matrik keputusan

Dalam prosedur ini, setiap atribut diubah menjadi nilai yang comparable.

Langkah 2: Pembobotan pada matrik yang telah dinormalisasi

Setelah dinormalisasi, setiap kolom dari matriks R dikalikan dengan bobot-bobot ( wi ) yang ditentukan oleh pembuat keputusan

Langkah 3 : Menetukan concordance dan discordance set.

Untuk setiap pasang dari alternative k dan l ( k,l = 1,2,3,…,m dan k ≠ l ) kumpulan kriteria Jdibagi menjadi 2 subsets, yaitu concordance dan discordance set. Bilamana sebuah kriteria dalam suatu alternative termasuk concordance adalah:

Ckl = { i, ykj e” ylj }, untuk I = 1,2,3,…,n

Sebaliknya, komplementer dari subset adalah Â discordance, yaitu bila:

Dkl = { i, ykj < Â ylj }, untuk I = 1,2,3,…,n

Langkah 4: Hitung matriks concordance 

adalah dengan menjumlahkan bobot-bobot yang termasuk dalam subset concordance

Langkah 5 : Menentukan matrik dominan Â concordance Â dan discordance

a. Concordance

Matrik dominan Concordance dapat dibangun dengan bantuan nilai threshold, yaitu dengan membandingkan setiap nilai elemen matriks Concordance dengan nilai threshold.

Ckl â‰¥ c

Dan nilai tiap elemen matriks F  sebagai matriks dominan concordance ditentukan sebagai berikut :

Fkl = Â 1, jika ckl â‰¥c dan fkl = 0, jika ckl < c

b. Discordance

Untuk membangun matriks dominan discordance Â juga menggunakan bantuan nilai threshold

Dan setiap elemen untuk matriks G sebagai matriks dominan discordance ditentukan sebagai berikut:

gkl = 01, jika ckl â‰¥ d dan gkl Â = 1, jika ckl < d

langkah 6 : Menentukan aggregate dominance matrix

Langkah selanjutnya adalah menentukan aggregate dominance matrix sebagai matriks E, yang setiap elemennnya merupakan perkalian antara elemen matriks F dengan elemen matriks G, sebagai berikut:

ekl = fkl x gkl

Langkah 7 : Eliminasi alternative yang less favorable.

Matriks E memberikan urutan pilihan dari setiap alternative, yaitu bila Â ekl = 1 maka alternative Ak merupakan piihan yang lebih baik daripada Ar sehingga baris dalam matriks E yang memiliki jumlah ekl = 1 paling sedikit dapat dieliminasi. Dengan demikian alternative terbaik adalah yang mendominas alternative lainnya.

sumber : http://kiky-riski.blogspot.com/2014/07/metode-electre-elimination-and-choice.html

Sistem Pendukung Keputusan Dengan Metode AHP

Metode AHP dikembangkan oleh Thomas L. Saaty, seorang ahli matematika. Metode ini adalah sebuah kerangka untuk mengambil keputusan dengan efektif atas persoalan yang kompleks dengan menyederhanakan dan mempercepat proses pengambilan keputusan dengan memecahkan persoalan tersebut kedalam bagian-bagiannya, menata bagian atau variabel ini dalam suatu susunan hirarki, member nilai numerik pada pertimbangan subjektif tentang pentingnya tiap variabel dan mensintesis berbagai pertimbangan ini untuk menetapkan variabel yang mana yang memiliki prioritas paling tinggi dan bertindak untuk mempengaruhi hasil pada situasi tersebut. Metode AHP ini membantu memecahkan persoalan yang kompleks dengan menstruktur suatu hirarki kriteria, pihak yang berkepentingan, hasil dan dengan menarik berbagai pertimbangan guna mengembangkan bobot atau prioritas. Metode ini juga menggabungkan kekuatan dari perasaan dan logika yang bersangkutan pada berbagai persoalan, lalu mensintesis berbagai pertimbangan yang beragam menjadi hasil yang cocok dengan perkiraan kita secara intuitif sebagaimana yang dipresentasikan pada pertimbangan yang telah dibuat. (Saaty, 1993).

Proses hierarki adalah suatu model yang memberikan kesempatan bagi perorangan atau kelompok untuk membangun gagasan-gagasan dan mendefinisikan persoalan dengan cara membuat asumsi mereka masing-masing dan memperoleh pemecahan yang diinginkan darinya. Ada dua alasan utama untuk menyatakan suatu tindakan akan lebih baik dibanding tindakan lain. Alasan yang pertama adalah pengaruh-pengaruh tindakan tersebut kadang-kadang tidak dapat dibandingkan karena sutu ukuran atau bidang yang berbeda dan kedua, menyatakan bahwa pengaruh tindakan tersebut kadang-kadang saling bentrok, artinya perbaikan pengaruh tindakan tersebut yang satu dapat dicapai dengan pemburukan lainnya. Kedua alasan tersebut akan menyulitkan dalam membuat ekuivalensi antar pengaruh sehingga diperlukan suatu skala luwes yang disebut prioritas.

Prinsip Dasar dan Aksioma AHP

AHP didasarkan atas 3 prinsip dasar yaitu:

1. Dekomposisi
Dengan prinsip ini struktur masalah yang kompleks dibagi menjadi bagian-bagian secara hierarki. Tujuan didefinisikan dari yang umum sampai khusus. Dalam bentuk yang paling sederhana struktur akan dibandingkan tujuan, kriteria dan level alternatif. Tiap himpunan alternatif mungkin akan dibagi lebih jauh menjadi tingkatan yang lebih detail, mencakup lebih banyak kriteria yang lain. Level paling atas dari hirarki merupakan tujuan yang terdiri atas satu elemen. Level berikutnya mungkin mengandung beberapa elemen, di mana elemen-elemen tersebut bisa dibandingkan, memiliki kepentingan yang hampir sama dan tidak memiliki perbedaan yang terlalu mencolok. Jika perbedaan terlalu besar harus dibuatkan level yang baru.
2. Perbandingan penilaian/pertimbangan (comparative judgments).
Dengan prinsip ini akan dibangun perbandingan berpasangan dari semua elemen yang ada dengan tujuan menghasilkan skala kepentingan relatif dari elemen. Penilaian menghasilkan skala penilaian yang berupa angka. Perbandingan berpasangan dalam bentuk matriks jika dikombinasikan akan menghasilkan prioritas.
3. Sintesa Prioritas
Sintesa prioritas dilakukan dengan mengalikan prioritas lokal dengan prioritas dari kriteria bersangkutan di level atasnya dan menambahkannya ke tiap elemen dalam level yang dipengaruhi kriteria. Hasilnya berupa gabungan atau dikenal dengan prioritas global yang kemudian digunakan untuk memboboti prioritas lokal dari elemen di level terendah sesuai dengan kriterianya.

AHP didasarkan atas 3 aksioma utama yaitu :

1. Aksioma Resiprokal
Aksioma ini menyatakan jika PC (EA,EB) adalah sebuah perbandingan berpasangan antara elemen A dan elemen B, dengan memperhitungkan C sebagai elemen parent, menunjukkan berapa kali lebih banyak properti yang dimiliki elemen A terhadap B, maka PC (EB,EA)= 1/ PC (EA,EB). Misalnya jika A 5 kali lebih besar daripada B, maka B=1/5 A.
2. Aksioma Homogenitas
Aksioma ini menyatakan bahwa elemen yang dibandingkan tidak berbeda terlalu jauh. Jika perbedaan terlalu besar, hasil yang didapatkan mengandung nilai kesalahan yang tinggi. Ketika hirarki dibangun, kita harus berusaha mengatur elemen-elemen agar elemen tersebut tidak menghasilkan hasil dengan akurasi rendah dan inkonsistensi tinggi.
3. Aksioma Ketergantungan
Aksioma ini menyatakan bahwa prioritas elemen dalam hirarki tidak bergantung pada elemen level di bawahnya. Aksioma ini membuat kita bisa menerapkan prinsip komposisi hirarki.

Kelebihan dan Kekurangan dalam Metode AHP

Kelebihan

1. Struktur yang berhierarki sebagai konskwensi dari kriteria yang dipilih sampai pada sub-sub kriteria yang paling dalam.

1. Memperhitungkan validitas sampai batas toleransi inkonsentrasi sebagai kriteria dan alternatif yang dipilih oleh para pengambil keputusan.

1. Memperhitungkan daya tahan atau ketahanan output analisis sensitivitas pengambilan keputusan.

Metode “pairwise comparison” AHP mempunyai kemampuan untuk memecahkan masalah yang diteliti multi obyek dan multi kriteria yang berdasar pada perbandingan preferensi dari tiap elemen dalam hierarki. Jadi model ini merupakan model yang komperehensif. Pembuat keputusan menetukan pilihan atas pasangan perbandingan yang sederhana, membengun semua prioritas untuk urutan alternatif. “ Pairwaise comparison” AHP mwenggunakan data yang ada bersifat kualitatif berdasarkan pada persepsi, pengalaman, intuisi sehigga dirasakan dan diamati, namun kelengkapan data numerik tidak menunjang untuk memodelkan secara kuantitatif.

Kelemahan

1. Ketergantungan model AHP pada input utamanya.

Input utama ini berupa persepsi seorang ahli sehingga dalam hal ini melibatkan subyektifitas sang ahli selain itu juga model menjadi tidak berarti jika ahli tersebut memberikan penilaian yang keliru.

1. Metode AHP ini hanya metode matematis tanpa ada pengujian secara statistik

sehingga tidak ada batas kepercayaan dari kebenaran model yang terbentuk

Tahapan Dalam Metode AHP

Langkah-langkah AHP

Langkah – langkah  dan proses Analisis Hierarki Proses (AHP) adalah sebagai berikut
1.       Memdefinisikan permasalahan dan penentuan tujuan. Jika AHP digunakan untuk memilih alternatif atau menyusun prioriras alternatif, pada tahap ini dilakukan pengembangan alternatif.
2.       Menyusun masalah kedalam hierarki sehingga permasalahan yang kompleks dapat ditinjau dari sisi yang detail dan terukur.
3.       Penyusunan prioritas untuk tiap elemen masalah pada hierarki. Proses ini menghasilkan bobot atau kontribusi elemen terhadap pencapaian tujuan sehingga elemen dengan bobot tertinggi memiliki prioritas penanganan. Prioritas dihasilkan dari suatu matriks perbandinagan berpasangan antara seluruh elemen pada tingkat hierarki yang sama.
4.       Melakukan pengujian konsitensi terhadap perbandingan antar elemen yang didapatan pada tiap tingkat hierarki.
Sedangkan langkah-langkah “pairwise comparison” AHP adalah
1.       Pengambilan data dari obyek yang diteliti.
2.       Menghitung data dari bobot perbandingan berpasangan responden dengan metode
“pairwise comparison” AHP berdasar hasil kuisioner.
3.       Menghitung rata-rata rasio konsistensi dari masing-masing responden.
4.       Pengolahan dengan metode “pairwise comparison” AHP.
5.      Setelah dilakukan pengolahan tersebut, maka dapat disimpulkan adanya konsitensi   dengan tidak, bila data tidak konsisten maka diulangi lagi dengan pengambilan data seperti semula, namun bila sebaliknya maka digolongkan data terbobot yang selanjutnya dapat dicari nilai beta (b).

Contoh Kasus

Adi berulang tahun yang ke-17, Kedua orang tuanya janji untuk membelikan sepeda motor sesuai yang di inginkan Adi. Adi memiliki pilihan yaitu motor Ninja, Tiger dan Vixsion . Adi memiliki criteria dalam pemilihan sepeda motor yang nantinya akan dia beli yaitu : sepeda motornya memiliki desain yang bagus, berkualitas serta irit dalam bahan bakar.
Penyelesaian

1. 1.     Tahap pertama

Menentukan botot dari masing – masig kriteria.

Desain lebih penting 2 kali dari pada Irit

Desain lebih penting 3 kali dari pada Kualitas

Irit lebih penting 1.5 kali dari pada kualitas

Pair Comparation Matrix

Kriteria	Desain	Irit	Kualitas	Priority Vector
Desain	1	2	3	0,5455
Irit	0,5	1	1,5	0,2727
Kualitas	0,333	0,667	1	0,1818
Jumlah	1,833	3,667	5,5	1,0000
Pricipal Eigen Value (lmax)				3,00
Consistency Index (CI)				0
Consistency Ratio (CR)				0,0%

Dari gambar diatas, Prioity Vector (kolom paling kanan) menunjukan bobot dari masing-masing kriteria, jadi dalam hal ini Desain merupakan bobot tertinggi/terpenting menurut Adi, disusul Irit dan yang terakhir adalah Kualitas.
Cara membuat table seperti di atas

1. Untuk perbandingan antara masing – masing kriteria berasal dari bobot yang telah di berikan ADI pertama kali.
2. Sedangkan untuk Baris jumlah, merupakan hasil penjumalahan vertikal dari masing – masing kriteria.
3. Untuk Priority Vector  di dapat dari  hasil penjumlahan dari semua sel disebelah Kirinya (pada baris yang sama) setelah terlebih dahulu dibagi dengan  Jumlah yang ada dibawahnya, kemudian hasil penjumlahan tersebut dibagi dengan angka 3.
4. Untuk mencari Principal Eigen Value (lmax)

Rumusnya adalah menjumlahkan  hasil perkalian antara sel pada baris jumlah dan sel pada kolom Priority Vector

5. Menghitung Consistency Index (CI) dengan rumus

CI = (lmax-n)/(n-1)

6. Sedangkan untuk menghitung nilai  CR
7. Menggunakan rumuas CR = CI/RI , nilai RI didapat dari

n	1	2	3	4	5	6	7	8	9	10
RI	0	0	5,8	0,9	1,12	1,24	1,32	1,41	1,45	1,49

Jadi untuk n=3, RI=0.58.
Jika hasil perhitungan  CR lebih kecil atau sama dengan 10% ,  ketidak konsistenan masih bisa diterima, sebaliknya jika lebih besar dari 10%, tidak bisa diterima.

1. 2.     Tahap Kedua

Kebetulan teman ADI memiliki teman yang memiliki motor yang sesuai dengan pilihan ADI. Setelah Adi mencoba motor temannya tersebut adi memberikan penilaian ( disebut sebagai pair-wire comparation)

Desain lebih penting 2 kali dari pada Irit

Desain lebih penting 3 kali dari pada Kualitas

Irit lebih penting 1.5 kali dari pada kualitas

Ninja  4 kali desainnya lebih baik daripada tiger

Ninja  3 kali desainnya lebih baik dari pada vixsion

tiger 1/2 kali desainnya lebih baik dari pada Vixsion

Ninja 1/3 kali lebih irit daripada tiger

Ninja 1/4 kali  lebih irit dari pada vixsion

tiger 1/2 kali lebih irit dari pada Vixsion

Berdasarkan penilaian tersebut maka dapat di buat table (disebut Pair-wire comparation matrix)

Desain	Ninja	Tiger	Vixsion	Priority Vector
Ninja	1	4	3	0,6233
Tiger	0,25	1	0,5	0,1373
Vixsion	0,333	2	1	0,2394
Jumlah	1,583	7	4,5	1,0000
Pricipal Eigen Value (lmax)				3,025
Consistency Index (CI)				0,01
Consistency Ratio (CR)				2,2%

Irit	Ninja	Tiger	Vixsion	Priority Vector
Ninja	1	0,333	0,25	0,1226
Tiger	3	1	0,5	0,3202
Vixsion	4	2	1	0,5572
Jumlah	8	3,333	1,75	1,0000
Pricipal Eigen Value (lmax)				3,023
Consistency Index (CI)				0,01
Consistency Ratio (CR)				2,0%

Irit	Ninja	Tiger	Vixsion	Priority Vector
Ninja	1,00	0,010	0,10	0,0090
Tiger	100,00	1,00	10,0	0,9009
Vixsion	10,00	0,100	1,0	0,0901
Jumlah	111,00	1,11	11,10	1,0000
Pricipal Eigen Value (lmax)				3
Consistency Index (CI)				0
Consistency Ratio (CR)				0,0%

1. 3.     Tahap ketiga

Setelah mendapatkan bobot untuk ketiga kriteria dan skor untuk masing-masing kriteria bagi ketiga motor pilihannya, maka langkah terakhir adalah menghitung total skor untuk ketiga motor tersebut.  Untuk itu ADI akan merangkum semua hasil penilaiannya tersebut dalam bentuk tabel yang disebut Overall composite weight, seperti berikut.

Overall composit weight	weight	Ninja	Tiger	Vixsion
Desain	0,5455	0,6233	0,1373	0,2394
Irit	0,2727	0,1226	0,3202	0,5572
Kualitas	0,1818	0,0090	0,9009	0,0901
Composit Weight		0,3751	0,3260	0,2989

Cara membuat Overall Composit weight adalah

• Kolom Weight diambil dari kolom Priority Vektor dalam matrix Kriteria.
• Ketiga kolom lainnya (Ninja, Tiger dan Vixsion) diambil dari kolom Priority Vector ketiga matrix Desain, Irit dan Kualitas.
• Baris Composite Weight diperoleh dari jumlah hasil perkalian sel diatasnya dengan weight.

Berdasarkan table di atas maka dapat di ambil kesimpulan bahwa yang memiliki skor paling tinggi adalah Ninja yaitu 0,3751 , sedangkan disusul tiger dengan skor 0,3260 dan yang terakhir adalah Vixsion dengan skor 0,2989. Akhirnya Adi akan membeli motor Ninja

sumber : https://annisafelayatie.wordpress.com/2012/10/30/makalah-sistem-pendukung-keputusan-dengan-metode-ahp/

Metode TOPSIS dalam Sistem Pendukung Keputusan (SPK)

Metode TOPSIS

Metode  TOPSIS  adalah  salah  satu  metode  pengambilan  keputusan multikriteria yang pertama kali diperkenalkan oleh Yoon dan Hwang  pada tahun 1981.  Metode  ini  merupakan  salah  satu  metode  yang  banyak  digunakan  untuk menyelesaikan pengambilan  keputusan  secara  praktis.  TOPSIS  memiliki  konsep dimana alternatif  yang terpilih merupakan alternatif terbaik  yang memiliki jarak terpendek dari solusi ideal positif dan jarak terjauh dari solusi ideal negatif [4]. Semakin  banyaknya  faktor  yang  harus  dipertimbangkan  dalam  proses pengambilan  keputusan,  maka  semakin  relatif  sulit  juga  untuk  mengambil
keputusan  terhadap  suatu  permasalahan.  Apalagi  jika  upaya  pengambilan keputusan  dari  suatu  permasalahan  tertentu,  selain  mempertimbangkan  berbagai faktor/kriteria  yang  beragam,  juga  melibatkan  beberapa  orang  pengambil keputusan.  Permasalahan  yang  demikian  dikenal  dengan  permasalahan  multiple criteria decision making  (MCDM).  Dengan kata lain, MCDM juga dapat disebut sebagai  suatu  pengambilan  keputusan  untuk  memilih  alternatif  terbaik  dari sejumlah  alternatif  berdasarkan  beberapa  kriteria  tertentu.  Metode  TOPSISdigunakan  sebagai  suatu  upaya  untuk  menyelesaikan  permasalahan  multiple criteria  decision  making.  Hal  ini  disebabkan  konsepnya  sederhana  dan  mudah dipahami, komputasinya  efisien  dan  memiliki  kemampuan  untuk  mengukur kinerja relatif dari alternatif-alternatif keputusan.

Langkah-langkah Metode TOPSIS

Langkah-langkah yang dilakukan dalam menyelesaikan suatu permasalahan menggunakan metode TOPSIS adalah sebagai berikut [4]:

1. Menggambarkan  alternatif  (m)  dan  kriteria  (n)  ke  dalam  sebuah  matriks, dimana  Xij adalah  pengukuran  pilihan  dari  alternatif  ke-i  dan  kriteria  ke-j.Matriks ini dapat dilihat pada persamaan satu.
    
2. Membuat matriks R yaitu matriks keputusan ternormalisasi Setiap  normalisasi  dari  nilai  rij dapat  dilakukan  dengan  perhitungan menggunakan persamaan dua.
   
3. Membuat pembobotan pada matriks yang telah dinormalisasi Setelah dinormalisasi, setiap kolom pada matriks R dikalikan dengan bobotbobot (wj) untuk menghasilkan matriks pada persamaan tiga.
   
4. Menentukan nilai solusi ideal positif dan solusi ideal negatif. Solusi ideal dinotasikan A+, sedangkan solusi ideal negatif dinotasikan A-. Persamaan untuk menentukan solusi ideal dapat dilihat pada persamaan empat.
   
5. Menghitung separation measure. Separation measure ini merupakan
   pengukuran jarak dari suatu alternatif ke solusi ideal positif dan solusi ideal
   negatif.
   –  Perhitungan solusi ideal positif dapat dilihat pada persamaan lima :
   
   –  Perhitungan solusi ideal negatif dapat dilihat pada persamaan enam :
6. Menghitung  nilai  preferensi  untuk  setiap  alternatif. Untuk  menentukan ranking tiap-tiap alternatif yang ada maka perlu dihitung terlebih dahulu nilai preferensi  dari  tiap  alternatif.  Perhitungan  nilai  preferensi  dapat  dilihat melalui persamaan tujuh.
   Setelah  didapat  nilai  Ci+,  maka  alternatif  dapat  diranking  berdasarkan urutan  Ci+.  Dari  hasil  perankingan  ini  dapat  dilihat  alternatif  terbaik  yaitu alternatif yang memiliki jarak terpendek dari solusi ideal dan berjarak terjauh dari solusi ideal negatif.

sumber : https://nerims.wordpress.com/2014/03/20/metode-topsis-dalam-sistem-pendukung-keputusan-spk/

Metode Weighted Product WP dalam Sistem Pendukung Keputusan (SPK)

Metode Weight Product (WP)
Metode  WP  mengunakan perkalian untuk menghubungkan rating atribut, di mana rating setiap atribut harus dipangkatkan dulu dengan bobot atribut yang bersangkutan.
Proses ini Ai diberikan sebagai berikut :

Dimana  ∑wj =  1.  wj  adalah  pangkat  bernilai  positif  untuk  atribut  keuntungan,  dan bernilai negatif untuk atribut biaya.
Preferensi relatif dari setiap alternatif, diberikan sebagai:

Contoh kasus :
Misalkan nilai setiap alternatif pada setiap atribut diberikan berdasarkan data riil yang ada seperti pada Tabel 2.1, perlu diidentifikasi terlebih dahulu jenis kriterianya, apakah termasuk kriteria keuntungan atau kriteria biaya.

Rating kecocokan dari setiap alternatif pada setiap kriteria
(Kusumadewi, Hartati, Harjoko, dan Wardoyo, 2006: 78)

Kriteria C2 (kepadatan penduduk di sekitar lokasi) dan C4 (jarak dengan gudang  yang sudah  ada)  adalah  criteria  keuntungan.  Sedangkan  kriteria  C1(jarak  dengan  pasar terdekat), C3 (jarak dari pabrik), dan C5 (harga tanah untuk lokasi) adalah kriteria biaya.Permasalahan kasus di atasakan di selesaikan dengan menggunakan metode  Weighted Product (WP). Sebelumnya akan dilakukan perbaikan bobot terlebih dahulu. Bobot awal W = (5, 3, 4, 4, 2), akan diperbaiki sehingga total bobot ∑Wj = 1, dengan cara :

Kemudian vektor S dihitung berdasarkan persamaan  dengan i = 1, 2, … ,m sebagai berikut :

Nilai  vektor  yang  akan  digunakan  untuk  perankingan  dapat  dihitung  berdasarkan persamaan

Nilai terbesar ada pada V2  sehingga alternatif A2 adalah alternatif yang terpilih sebagai alternatif  terbaik.  Dengan  kata  lain,  alternatif  A2 akan  terpilih  sebagai  lokasi  untuk mendirikan gudang baru. ( Kusumadewi, Hartati, Harjoko, dan Wardoyo, 2006: 79 )

 sumber : https://nerims.wordpress.com/2014/03/20/metode-weighted-product-wp-dalam-sistem-pendukung-keputusan-spk/

Penerapan Metode SAW

Metode sistem pendukung keputusan SAW (Simple additive Weighting) merupakan salah satu metode Sistem Pendukung Keputusan yang menggunakan konsep penjumlahan terbobot. Pada tulisan kali ini saya akan memberikan contoh bagaimana cara Penerapan Metode Sistem Pendukung Keputusan SAW dengan PHP. Sebelumnya saya akan menjelaskan proses dari metode Simple additive weighting :

1. Siapkan terlebih dahulu data yang disimpan dalam Matrik Data.
2. Lakukan Normalisasi Matrik Data dengan formula :

Normalisasi Matrik SAW

3. Lakukan perangkingan dengan Formula

1	Vi = (rij * wi) + (rij * wi) + .. (rxx * wx)

Sebagai bahan Penerapan Metode SAW, berikut contoh kasus yang akan kita coba lakukan perhitungan dengan PHP.

Suatu Institusi Perguruan tinggi akan memilih seorang karyawan untuk dipromosikan sebagai kepala unit Sistem Informasi.

Ada empat kriteria yang digunakan untuk melakukan penilaian yaitu :

1.      C1  = Tes Pengetahuan (Wawasan) Sistem Informasi.

2.      C2 = Praktik Insatalasi Jaringan

3.      C3 = Tes Kepripadian

4.      C4 = Tes Pengetahuan Agama.

Pengambil keputusan memberikan bobot untuk setiap kriteria sebagai berikut: C1 = 35%; C2 = 25%; C3 = 25%; dan C4 = 15%.

Ada enam orang karyawan yang menjadi kandidat (alternatif) untuk dipromosikan sebagai kepala unit, yaitu:

1.      A1 = Indra

2.      A2 = Roni,

3.      A3 = Putri,

4.      A4 = Dani,

5.      A5 = Ratna, dan

6.      A6 = Mira.

Data diatas sekarang kita rubah ke dalam database, buat database kira2 seperti ini :

tbcalon :

Tabel Calon Sistem Pendukung Keputusan

Selanjutnya kita buat tabel untuk menyimpan matrik, misal tbmatrik :

Tabel Matrik Sistem Pendukung Keputusan

Setelah keduanya dibuat, silahkan isi data sehingga terbentuk data seperti ini :
tbcalon :

Data Calon SPK

dan data Matrik :

Data Matrik Calon SPK

Langkah-langkah perhitungan sistem pendukung keputusan dengan php :

Lakukan Langkah ke 2, yakni normalisasi :

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

//Lakukan Normalisasi dengan rumus pada langkah 2     //Cari Max atau min dari tiap kolom Matrik     $crMax = mysql_query("SELECT max(Kriteria1) as maxK1,                         max(Kriteria2) as maxK2,                         max(Kriteria3) as maxK3,                         max(Kriteria4) as maxK4             FROM tbmatrik");     $max = mysql_fetch_array($crMax);     //Hitung Normalisasi tiap Elemen     $sql2 = mysql_query("SELECT * FROM tbmatrik");     //Buat tabel untuk menampilkan hasil     echo "<H3>Matrik Normalisasi</H3>     <table width=500 style='border:1px; #ddd; solid; border-collapse:collapse' border=1>         <tr>             <td>No</td><td>Nama</td><td>C1</td><td>C2</td><td>C3</td><td>C4</td>         </tr>         ";     $no = 1;     while ($dt2 = mysql_fetch_array($sql2)) {         echo "<tr>             <td>$no</td><td>".getNama($dt2['idCalon'])."</td><td>".round($dt2['Kriteria1']/$max['maxK1'],2)."</td><td>".round($dt2['Kriteria2']/$max['maxK2'],2)."</td><td>".round($dt2['Kriteria3']/$max['maxK3'],2)."</td><td>".round($dt2['Kriteria4']/$max['maxK4'],2)."</td>         </tr>";     $no++;     }     echo "</table>";

Selanjutnya lakukan Perangkingan :

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

//Proses perangkingan dengan rumus langkah 3     $sql3 = mysql_query("SELECT * FROM tbmatrik");     //Buat tabel untuk menampilkan hasil     echo "<H3>Perangkingan</H3>     <table width=500 style='border:1px; #ddd; solid; border-collapse:collapse' border=1>         <tr>             <td>No</td><td>Nama</td><td>Rangking</td>         </tr>         ";     $no = 1;     //Kita gunakan rumus (Normalisasi x bobot)     while ($dt3 = mysql_fetch_array($sql3)) {         echo "<tr>             <td>$no</td><td>".getNama($dt3['idCalon'])."</td>             <td>"             .round((($dt3['Kriteria1']/$max['maxK1'])*$bobot[0])+             (($dt3['Kriteria2']/$max['maxK2'])*$bobot[1])+             (($dt3['Kriteria3']/$max['maxK3'])*$bobot[2])+             (($dt3['Kriteria4']/$max['maxK4'])*$bobot[3]),2)."</td>         </tr>";     $no++;     }     echo "</table>";

Selesai, berikut adalah perhitungan sistem pendukung keputusan dengan PHP :

Hasil Sistem Pendukung Keputusan

http://burhanudin.web.id/programing/penerapan-metode-sistem-pendukung-keputusan-saw