Tiafani Hutabarat: Metode TOPSIS dalam Sistem Pendukung Keputusan (SPK)

Metode TOPSIS

Metode TOPSIS adalah salah satu metode pengambilan keputusan multikriteria yang pertama kali diperkenalkan oleh Yoon dan Hwang pada tahun 1981. Metode ini merupakan salah satu metode yang banyak digunakan untuk menyelesaikan pengambilan keputusan secara praktis. TOPSIS memiliki konsep dimana alternatif yang terpilih merupakan alternatif terbaik yang memiliki jarak terpendek dari solusi ideal positif dan jarak terjauh dari solusi ideal negatif [4]. Semakin banyaknya faktor yang harus dipertimbangkan dalam proses pengambilan keputusan, maka semakin relatif sulit juga untuk mengambil
keputusan terhadap suatu permasalahan. Apalagi jika upaya pengambilan keputusan dari suatu permasalahan tertentu, selain mempertimbangkan berbagai faktor/kriteria yang beragam, juga melibatkan beberapa orang pengambil keputusan. Permasalahan yang demikian dikenal dengan permasalahan multiple criteria decision making (MCDM). Dengan kata lain, MCDM juga dapat disebut sebagai suatu pengambilan keputusan untuk memilih alternatif terbaik dari sejumlah alternatif berdasarkan beberapa kriteria tertentu. Metode TOPSISdigunakan sebagai suatu upaya untuk menyelesaikan permasalahan multiple criteria decision making. Hal ini disebabkan konsepnya sederhana dan mudah dipahami, komputasinya efisien dan memiliki kemampuan untuk mengukur kinerja relatif dari alternatif-alternatif keputusan.

Langkah-langkah Metode TOPSIS

Langkah-langkah yang dilakukan dalam menyelesaikan suatu permasalahan menggunakan metode TOPSIS adalah sebagai berikut [4]:

Menggambarkan alternatif (m) dan kriteria (n) ke dalam sebuah matriks, dimana Xij adalah pengukuran pilihan dari alternatif ke-i dan kriteria ke-j.Matriks ini dapat dilihat pada persamaan satu.
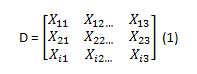
Membuat matriks R yaitu matriks keputusan ternormalisasi Setiap normalisasi dari nilai rij dapat dilakukan dengan perhitungan menggunakan persamaan dua.
Membuat pembobotan pada matriks yang telah dinormalisasi Setelah dinormalisasi, setiap kolom pada matriks R dikalikan dengan bobotbobot (wj) untuk menghasilkan matriks pada persamaan tiga.
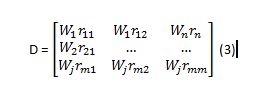
Menentukan nilai solusi ideal positif dan solusi ideal negatif. Solusi ideal dinotasikan A+, sedangkan solusi ideal negatif dinotasikan A-. Persamaan untuk menentukan solusi ideal dapat dilihat pada persamaan empat.
Menghitung separation measure. Separation measure ini merupakan
pengukuran jarak dari suatu alternatif ke solusi ideal positif dan solusi ideal
negatif.
– Perhitungan solusi ideal positif dapat dilihat pada persamaan lima :

– Perhitungan solusi ideal negatif dapat dilihat pada persamaan enam :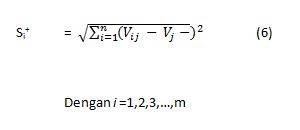
Menghitung nilai preferensi untuk setiap alternatif. Untuk menentukan ranking tiap-tiap alternatif yang ada maka perlu dihitung terlebih dahulu nilai preferensi dari tiap alternatif. Perhitungan nilai preferensi dapat dilihat melalui persamaan tujuh.
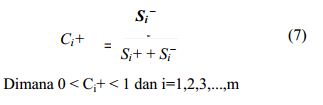Setelah didapat nilai Ci+, maka alternatif dapat diranking berdasarkan urutan Ci+. Dari hasil perankingan ini dapat dilihat alternatif terbaik yaitu alternatif yang memiliki jarak terpendek dari solusi ideal dan berjarak terjauh dari solusi ideal negatif.